It is often said that computers "talk to each other in 1s and 0s" (or bits), but the details of how we can represent something interesting like a video as a sequence of digits in an efficient manner are often left unexplained. 

This blog aims to shed some light on the technology at the heart of video compression: entropy coding. To get there, we will explore the answers to:

• How are digital images displayed?
• How can we exploit repeating patterns as a form of simple lossless compression?
• Why does better knowledge of the frequencies of different symbols result in better compression?
• How do modern compression algorithms theoretically allow you to efficiently store anything in a single number (if you have enough precision)?

What's in an image?

First, a whistle-stop tour of the fundamentals:

When you look at a digital image being displayed on a screen, you are seeing what we call a bitmap. The screen consists of many pixels organised into rows, and each pixel displays a colour. For simplicity, we're going to think about greyscale (black and white) images, but if you're interested in the complexities of dealing with colour, check out this blog. Typically, each pixel will be able to display one of 256 shades of grey, represented by a sequence of 8 bits (one byte) from 00000000 (black) to 11111111 (white). Even though the image is two-dimensional, the data is actually one-dimensional. Usually (but not always), it is arranged in "raster-scan order", where we read rows from left to right one at a time from top to bottom. Here is an illustration of this order on a rather sad version of the Deep Render logo that has been resized to 32x32 pixels:

We will think of each of these 256 possibilities as being separate symbols for the purposes of encoding. Here is the same image above, but instead labelled with its colour values.

We use hexadecimal code (base 16) to display the 256 possible values, as 8 binary digits are hard to squeeze into a pixel! This uses the digits 0-9 and the letters a-f to represent numbers between 0 and 15, meaning that you can represent all integers between 0 and 255 with two characters: 0 becomes 00 (0 * 16 + 0* 1), 100 becomes 64 (6 * 16 + 4 * 1) and 255 becomes ff (15 * 16 + 15 * 1).

The original 32x32 image (without labelling) can be found below:

In total, as illustrated above, it contains 1024 pixels and therefore takes just over 1KB to store as a bitmap. A Full HD image contains over 2 million pixels and therefore takes over 2 million bytes (2MB) to store as a bitmap. However, if you download this Full HD image, you will find that it actually only takes up a mere 10 thousand bytes to store:

Description: the image above is a white square

The .png file contains all of the information needed to perfectly reconstruct the image (i.e. it has been losslessly compressed), but requires 200 times less storage space than what we worked out for the bitmap! How is this possible?

Repetition = redundancy

As you may have noticed, it isn't a very interesting image. If you wanted to describe it to a friend, you wouldn't describe each of the two million white pixels individually, but you would instead describe them as a block. It is possible to do something very similar when storing an image. Instead of actually writing out 11111111, 11111111, ... two million times, we can instead just say repeat 11111111 two million times and save huge amounts of storage. This is known as run length encoding (RLE) [1], where "run length" refers to the fact that we store how long the run of repeating bytes is. With this technique, we could actually store our completely white image with far fewer bytes than the 10 thousand used in the example! Let's see how it fares on our logo image from above

Repeat 00 4 times
Repeat 80 1 times
Repeat 7f 6 times
Repeat 7d 1 times
Repeat 7f 17 times
Repeat 00 7 times
Repeat 7a 25 times
Repeat 00 5 times
Repeat 7a 28 times
Repeat 7d 1 times
Repeat 00 3 times
Repeat 7a 28 times
Repeat 7d 1 times
Repeat 00 1 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 3 times
Repeat 7b 2 times
Repeat 7a 5 times
Repeat 7b 1 times
Repeat 7a 5 times
Repeat 7b 1 times
Repeat 7a 14 times
Repeat 7d 1 times
Repeat 7a 3 times
Repeat 7b 3 times
Repeat 7d 1 times
Repeat 7b 1 times
Repeat 7d 1 times
Repeat 7b 4 times
Repeat 7a 3 times
Repeat 7b 8 times
Repeat 7a 7 times
Repeat 7d 1 times
Repeat 7a 3 times
Repeat 7b 2 times
Repeat 15 1 times
Repeat 17 2 times
Repeat 15 2 times
Repeat 17 2 times
Repeat 15 1 times
Repeat 7a 3 times
Repeat 14 1 times
Repeat 17 1 times
Repeat 15 6 times
Repeat 6f 1 times
Repeat 7a 6 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 51 1 times
Repeat 59 1 times
Repeat 5a 1 times
Repeat 59 2 times
Repeat 5a 1 times
Repeat 59 1 times
Repeat 35 1 times
Repeat 4e 1 times
Repeat 7a 1 times
Repeat 14 1 times
Repeat 15 1 times
Repeat 59 6 times
Repeat 39 1 times
Repeat 35 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7c 1 times
Repeat 15 1 times
Repeat 6c 1 times
Repeat 7a 5 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 1 times
Repeat 15 1 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 15 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 17 1 times
Repeat 6d 1 times
Repeat 7a 6 times
Repeat 15 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 1 times
Repeat 15 1 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 15 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7c 1 times
Repeat 15 1 times
Repeat 6d 1 times
Repeat 7a 6 times
Repeat 15 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 2 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 15 1 times
Repeat 7b 1 times
Repeat 7a 4 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 6d 1 times
Repeat 7a 6 times
Repeat 17 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 1 times
Repeat 15 1 times
Repeat 14 1 times
Repeat 15 1 times
Repeat 14 2 times
Repeat 15 1 times
Repeat 14 1 times
Repeat 70 1 times
Repeat 7b 1 times
Repeat 7a 5 times
Repeat 7c 1 times
Repeat 7b 5 times
Repeat 15 1 times
Repeat 6c 1 times
Repeat 7a 6 times
Repeat 15 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 1 times
Repeat 16 1 times
Repeat 14 5 times
Repeat 15 1 times
Repeat 70 1 times
Repeat 7b 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 1 times
Repeat 7b 1 times
Repeat 7a 1 times
Repeat 7b 2 times
Repeat 15 1 times
Repeat 6c 1 times
Repeat 7a 6 times
Repeat 16 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 2 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 16 2 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 1 times
Repeat 7b 2 times
Repeat 7a 1 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 6c 1 times
Repeat 7a 1 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 15 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 2 times
Repeat 7a 5 times
Repeat 5a 1 times
Repeat 1c 1 times
Repeat 15 1 times
Repeat 7a 5 times
Repeat 7c 1 times
Repeat 7a 3 times
Repeat 7b 2 times
Repeat 15 1 times
Repeat 6d 1 times
Repeat 7a 6 times
Repeat 16 1 times
Repeat 3a 1 times
Repeat 7a 1 times
Repeat 14 2 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 16 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 15 1 times
Repeat 4c 1 times
Repeat 57 2 times
Repeat 55 2 times
Repeat 54 1 times
Repeat 58 1 times
Repeat 38 1 times
Repeat 50 1 times
Repeat 7a 1 times
Repeat 14 2 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 15 1 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 4 times
Repeat 7b 1 times
Repeat 17 2 times
Repeat 15 3 times
Repeat 16 1 times
Repeat 15 2 times
Repeat 7a 3 times
Repeat 14 2 times
Repeat 7a 6 times
Repeat 20 1 times
Repeat 15 1 times
Repeat 7a 5 times
Repeat 7c 1 times
Repeat 7a 5 times
Repeat 7b 8 times
Repeat 7a 3 times
Repeat 7c 1 times
Repeat 7b 1 times
Repeat 7a 6 times
Repeat 7b 2 times
Repeat 7a 5 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 7d 1 times
Repeat 7a 63 times
Repeat 7d 1 times
Repeat 7a 31 times
Repeat 00 2 times
Repeat 7a 28 times
Repeat 7d 1 times
Repeat 00 3 times
Repeat 7a 7 times
Repeat 7b 1 times
Repeat 7a 15 times
Repeat 7b 1 times
Repeat 7a 4 times
Repeat 7d 1 times
Repeat 00 5 times
Repeat 7a 25 times
Repeat 00 3 times

Counting up the pairs of run lengths and symbols gives a total of 265 pairs. If we use one byte to store each run length and one to store each symbol, we will spend two bytes per pair, or 530 bytes in total. This is over half the bytes required to just store it as a bitmap, which seems disappointing. On closer inspection, we see that even though the rows of 7a values are being encoded well, there are often other values in the very first column of each row, breaking up the run of 7as. We'll see if we can do better.

Full HD images are rarely as simple as a blank white screen. A trickier example might look more like this:

If you zoom in, you will see that here we only have runs of 8 pixels of the same colour in a row, dashing the hopes of run length encoding. However, you also might notice that this image only takes up 68 thousand bytes of space, still well short of the 2 million required for a bitmap. What gives?

If you look closely, you will notice that while there is not a great deal of structure in the image, there is still some structure: the image is actually made up of 8x8 patches of one of the 256 shades of grey. Run length encoding can't capture this very well, but a more advanced method wouldn't just look for repeating patterns of a single byte and would instead try and find some repeating chunks of bytes that can be cut and pasted to make up the whole image — a bit like a collage! This is the key idea behind the LZ77 encoding algorithm [2].

Applying this algorithm to our logo image gives us output like this:

In position 0: 00
In position 1: Go back 1 symbols, copy 3 symbols followed by a 80
In position 5: 7f
In position 6: Go back 1 symbols, copy 5 symbols followed by a 7d
In position 12: Go back 7 symbols, copy 6 symbols followed by a 7f
In position 19: Go back 7 symbols, copy 10 symbols followed by a 00
In position 30: Go back 1 symbols, copy 6 symbols followed by a 7a
In position 37: Go back 1 symbols, copy 24 symbols followed by a 00
In position 62: Go back 30 symbols, copy 29 symbols followed by a 7a
In position 92: Go back 56 symbols, copy 2 symbols followed by a 7d
In position 95: Go back 32 symbols, copy 33 symbols followed by a 7d
In position 129: Go back 63 symbols, copy 28 symbols followed by a 7a
In position 158: Go back 66 symbols, copy 3 symbols followed by a 7a
In position 162: Go back 32 symbols, copy 98 symbols followed by a 7b
In position 261: 7b
In position 262: Go back 226 symbols, copy 5 symbols followed by a 7b
In position 268: Go back 6 symbols, copy 11 symbols followed by a 7a
In position 280: Go back 32 symbols, copy 14 symbols followed by a 7b
In position 295: 7d
In position 296: Go back 2 symbols, copy 3 symbols followed by a 7b
In position 300: Go back 40 symbols, copy 5 symbols followed by a 7b
In position 306: Go back 1 symbols, copy 7 symbols followed by a 7a
In position 314: Go back 64 symbols, copy 12 symbols followed by a 15
In position 327: 17
In position 328: 17
In position 329: 15
In position 330: Go back 4 symbols, copy 4 symbols followed by a 7a
In position 335: Go back 256 symbols, copy 2 symbols followed by a 14
In position 338: Go back 10 symbols, copy 3 symbols followed by a 15
In position 342: Go back 3 symbols, copy 3 symbols followed by a 6f
In position 346: Go back 192 symbols, copy 11 symbols followed by a 7b
In position 358: 15
In position 359: 51
In position 360: 59
In position 361: 5a
In position 362: 59
In position 363: Go back 3 symbols, copy 3 symbols followed by a 35
In position 367: 4e
In position 368: Go back 32 symbols, copy 2 symbols followed by a 15
In position 371: Go back 9 symbols, copy 2 symbols followed by a 59
In position 374: Go back 3 symbols, copy 3 symbols followed by a 39
In position 378: 35
In position 379: Go back 224 symbols, copy 10 symbols followed by a 7c
In position 390: 15
In position 391: 6c
In position 392: Go back 130 symbols, copy 6 symbols followed by a 15
In position 399: 3a
In position 400: Go back 32 symbols, copy 3 symbols followed by a 7a
In position 404: Go back 256 symbols, copy 5 symbols followed by a 20
In position 410: Go back 8 symbols, copy 6 symbols followed by a 7d
In position 417: Go back 154 symbols, copy 5 symbols followed by a 17
In position 423: 6d
In position 424: Go back 256 symbols, copy 6 symbols followed by a 15
In position 431: Go back 32 symbols, copy 22 symbols followed by a 7c
In position 454: 15
In position 455: Go back 32 symbols, copy 11 symbols followed by a 14
In position 467: Go back 64 symbols, copy 8 symbols followed by a 7b
In position 476: Go back 128 symbols, copy 11 symbols followed by a 6d
In position 488: Go back 256 symbols, copy 6 symbols followed by a 17
In position 495: Go back 96 symbols, copy 4 symbols followed by a 14
In position 500: Go back 2 symbols, copy 2 symbols followed by a 14
In position 503: Go back 5 symbols, copy 2 symbols followed by a 70
In position 506: Go back 245 symbols, copy 6 symbols followed by a 7c
In position 513: Go back 208 symbols, copy 5 symbols followed by a 15
In position 519: Go back 128 symbols, copy 6 symbols followed by a 7a
In position 526: Go back 128 symbols, copy 4 symbols followed by a 16
In position 531: Go back 66 symbols, copy 2 symbols followed by a 14
In position 534: Go back 33 symbols, copy 3 symbols followed by a 70
In position 538: Go back 226 symbols, copy 6 symbols followed by a 7d
In position 545: Go back 254 symbols, copy 2 symbols followed by a 7a
In position 548: Go back 32 symbols, copy 10 symbols followed by a 16
In position 559: Go back 96 symbols, copy 8 symbols followed by a 7b
In position 568: 15
In position 569: 16
In position 570: 16
In position 571: Go back 32 symbols, copy 8 symbols followed by a 7b
In position 580: Go back 224 symbols, copy 3 symbols followed by a 6c
In position 584: Go back 233 symbols, copy 6 symbols followed by a 15
In position 591: Go back 128 symbols, copy 9 symbols followed by a 5a
In position 601: 1c
In position 602: Go back 200 symbols, copy 6 symbols followed by a 7c
In position 609: Go back 255 symbols, copy 4 symbols followed by a 7b
In position 614: Go back 160 symbols, copy 8 symbols followed by a 16
In position 623: Go back 160 symbols, copy 11 symbols followed by a 16
In position 635: Go back 224 symbols, copy 11 symbols followed by a 15
In position 647: 4c
In position 648: 57
In position 649: 57
In position 650: 55
In position 651: 55
In position 652: 54
In position 653: 58
In position 654: 38
In position 655: 50
In position 656: Go back 192 symbols, copy 11 symbols followed by a 7a
In position 668: Go back 256 symbols, copy 11 symbols followed by a 17
In position 680: 15
In position 681: Go back 1 symbols, copy 2 symbols followed by a 16
In position 684: Go back 4 symbols, copy 2 symbols followed by a 7a
In position 687: Go back 252 symbols, copy 2 symbols followed by a 14
In position 690: Go back 32 symbols, copy 14 symbols followed by a 7c
In position 705: Go back 249 symbols, copy 5 symbols followed by a 7b
In position 711: Go back 1 symbols, copy 7 symbols followed by a 7a
In position 719: Go back 209 symbols, copy 4 symbols followed by a 7a
In position 724: Go back 19 symbols, copy 7 symbols followed by a 7a
In position 732: Go back 256 symbols, copy 9 symbols followed by a 7a
In position 742: Go back 5 symbols, copy 26 symbols followed by a 7d
In position 769: Go back 32 symbols, copy 95 symbols followed by a 7a
In position 865: Go back 128 symbols, copy 63 symbols followed by a 00
In position 929: 00
In position 930: Go back 190 symbols, copy 29 symbols followed by a 00
In position 960: Go back 32 symbols, copy 9 symbols followed by a 7b
In position 970: Go back 233 symbols, copy 15 symbols followed by a 7b
In position 986: Go back 32 symbols, copy 8 symbols followed by a 00
In position 995: Go back 66 symbols, copy 26 symbols followed by a 00
In position 1022: Go back 94 symbols, copy 2 symbols and stop

This is a sequence of 116 instructions, with each instruction consisting of up to three things: a distance to go back, a length of symbols to copy and what the next symbol is. If we use one byte to store each of them (allowing distances and lengths up to 256), we will use 348 bytes in total: a substantial improvement over the 530 used for run length encoding! We could certainly do a little better if we were smarter about how many bits we used to store each part of the instruction, but we'll leave it there for now.

Guess Who? Probability modelling for compression

A different, complementary approach is to think about the storage used for the symbols themselves. There are 256 possible bytes, but some of them might appear much more frequently in an image than others — in the extreme case of the white image, we only use 1 of these 256 possibilities! We could instead try and save space by using shorter codes for the most common symbols. This is how Morse code was designed to be efficient: the more common letters are given shorter codes (in terms of duration) so that messages can be transmitted quickly.

This general approach is known as entropy coding and is an important form of lossless compression. A piece of mathematics called Shannon's source coding theorem[3] tells us that there is a fundamental limit to how much you can compress a stream of symbols that come from some probability distribution (such as a sequence of dice rolls from a weighted die). The better we know the probability distribution (for instance, if we had studied the die and worked out which number came up more often), the closer we can get to this limit.

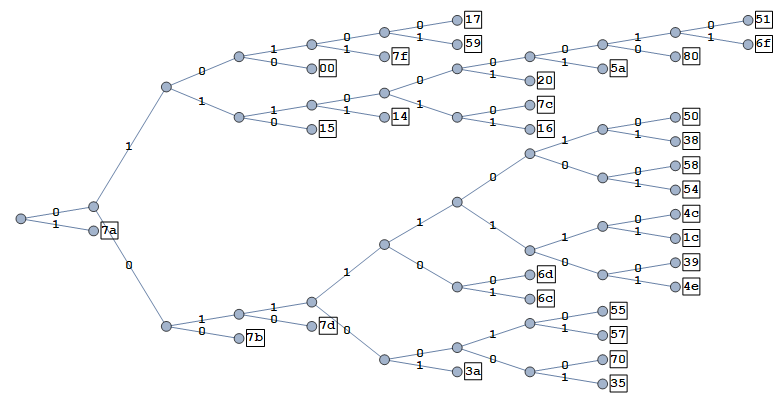
This is most easily achieved by the application of a method called Huffman coding [4]. This algorithm analyses the frequencies of different symbols and constructs a binary tree that specifies which codewords should be given to which symbols. You can think of this like trying to design a strategy to play the game Guess Who with an expanded deck of cards that contains some duplicates: if you know some characters are more likely than others, you can try and ask questions that focus on those characters first.

Applying the algorithm to our logo image gives the following table of frequencies and codewords.

symbol  | frequency | codeword
7a      | 0.718     | 1
7b      | 0.057     | 000
15      | 0.042     | 0110
00      | 0.032     | 0100
7d      | 0.028     | 0010
14      | 0.026     | 01111
7f      | 0.022     | 01011
59      | 0.010     | 010101
17      | 0.009     | 010100
3a      | 0.008     | 001101
16      | 0.007     | 0111011
7c      | 0.006     | 0111010
20      | 0.006     | 0111001
6c      | 0.004     | 0011101
6d      | 0.004     | 0011100
5a      | 0.003     | 01110001
35      | 0.002     | 00110001
70      | 0.002     | 00110000
57      | 0.002     | 00110011
55      | 0.002     | 00110010
80      | 0.001     | 011100000
6f      | 0.001     | 0111000011
51      | 0.001     | 0111000010
4e      | 0.001     | 001111101
39      | 0.001     | 001111100
1c      | 0.001     | 001111111
4c      | 0.001     | 001111110
54      | 0.001     | 001111001
58      | 0.001     | 001111000
38      | 0.001     | 001111011
50      | 0.001     | 001111010

Visualised in a tree:

Translating the symbols into binary using the table gives us the encoded version:

0100010001000100011100000010110101101011010110101101011001001011010110101101011010110101101011010110101101011010110101101011010110101101011010110100010001000100010001000100111111111111111111111111101000100010001000100111111111111111111111111111100100100010001001111111111111111111111111111001001000010111111111111111111111111111111100101111111111111111111111111111111001011111111111111111111111111111110010111111111111111111111111111111100101110000001111100011111000111111111111110010111000000000001000000100000000000001110000000000000000000000001111111001011100000001100101000101000110011001010001010001101110111101010001100110011001100110011001110000111111110010111100001100111000010010101011100010101010101010111000101010100110001001111101101111011001010101010101010101010101010101010100111110000110001111110010111101110100110001110111111000011000110110111101101111110111001011011111001011110000101000011100111111011000110110111101101111110111001011011111001011110111010011000111001111110110001101101111011111111110111001011000011110010111100001100011100111111010100001101101111011001111011001111011110110011110011000000011111011101000000000000000001100011101111111011000110110111101110110111101111011110111101111011000110000000111110010100010000000110001110111111101110110011011011110111111110000110011101101110111111100101000000100001100011101100101111011000110110111101111111110111000100111111101101111101110101110000000110001110011111101110110011011011110111111111101110010111011111110010111100001100011111100011001100110011001100100011001000111100100111100000111101100111101010111101111111111011100101101111100101111000010100010100011001100110011101101100110111011110111111111101110010110111110111010111110000000000000000000000001110111010000111111000000111110010111111111111111111111111111111100101111111111111111111111111111111001011111111111111111111111111111110010111111111111111111111111111111111111111111111111111111111111111001011111111111111111111111111111110100010011111111111111111111111111110010010001000100111111100011111111111111100011110010010001000100010001001111111111111111111111111010001000100

This is 2119 bits long, or just under 265 bytes, which beats our previous record from LZ77! However, we have cheated slightly: the true cost should also include the number of bytes used to store the frequency table. Nevertheless, this should hopefully illustrate the powerful principle.

Notice that the way in which the tree is constructed means that it is never ambiguous where the boundaries between codewords lie: with codewords 1, 000, 0110, 0100, there is only one way to parse the stream 00011110110000: 000 1 1 1 1 0110 000.

The methods above can be combined to great effect. If you've ever used a .zip file or a .png file like the one at the start of this blog, it probably used the DEFLATE algorithm to compress its contents, which combines Huffman coding with LZ77. .jpg files typically use a combination of Huffman coding with RLE*. These methods are relatively easy to carry out, but aren't always able to get close to the theoretical maximum level of compression. To do this, we will have to move away from methods that rely on encoding each symbol separately.

Taking a holistic view: an entire message in a single number (or two)

The canonical coding method that takes this approach is arithmetic coding (AC) [5]. This algorithm stores an entire message as a number between 0 and 1. More likely messages (as determined by the frequencies of the individual symbols in them) are stored as numbers with fewer digits after the decimal† point. This is achieved by the following steps until the entire message has been processed, beginning with the entire interval [0, 1]:

1. take the current interval and divide it according to the frequencies of the different symbols
2. identify the sub-interval that corresponds to the current symbol to be encoded
3. set the current interval as this sub-interval and go back to step 1.

Once all symbols have been processed, we are left with an interval, and we can pick the number within it with the shortest binary representation as our encoded message.

Going back to our favourite logo example, let's have a look at the frequency table that we used for Huffman encoding. We've added a new column for the cumulative frequency (the sum of all previous frequencies). As before, not all digits of precision are shown.

symbol | frequency | cumulative frequency
7a     | 0.718     | 0.718
7b     | 0.057     | 0.774
15     | 0.042     | 0.816
00     | 0.032     | 0.849
7d     | 0.028     | 0.877
14     | 0.026     | 0.903
7f     | 0.022     | 0.926
59     | 0.010     | 0.936
17     | 0.009     | 0.944
3a     | 0.008     | 0.952
16     | 0.007     | 0.959
7c     | 0.006     | 0.965
20     | 0.006     | 0.971
6c     | 0.004     | 0.975
6d     | 0.004     | 0.979
5a     | 0.003     | 0.981
35     | 0.002     | 0.983
70     | 0.002     | 0.985
57     | 0.002     | 0.987
55     | 0.002     | 0.989
80     | 0.001     | 0.990
6f     | 0.001     | 0.991
51     | 0.001     | 0.992
4e     | 0.001     | 0.993
39     | 0.001     | 0.994
1c     | 0.001     | 0.995
4c     | 0.001     | 0.996
54     | 0.001     | 0.997
58     | 0.001     | 0.998
38     | 0.001     | 0.999
50     | 0.001     | 1.000

If the first symbol is a 7a, we will end up with a number between 0.0 and approximately 0.718. If it's 7b, it will be between 0.718 and 0.774 and so on. In actual fact, our first pixel has a symbol of 00, so the eventual number will be between 0.816 and 0.849. We then take this interval and subdivide it again according to the same ratios and keep going until we run out of pixels. Eventually, we will arrive at a number that begins 0.843592489..., or in binary, 0.1101011111110.... In total, we will need 244 bytes to store the whole message, slightly edging out the 265 from our Huffman example. Again, we have slightly cheated by not including the storage cost of the frequencies, but this can be accounted for. There are some other simplications we have made such as assuming that we can work with as many digits of precision as we like when computing our intermediate results, but I will leave these to the interested reader to chase up!

This method is essentially as good as it gets (in terms of compression performance) for a fixed set of symbol frequencies. However, it can be pushed further by making the frequency table adaptive. If you can make a good guess about the probability distribution of the next symbol by looking at the previous ones and update your frequency table, you can achieve shorter message lengths overall. This is the idea behind context adaptive binary arithmetic coding (CABAC), which is the method of choice for most traditional video compression codecs‡.

Arithmetic coding achieves excellent compression performance, but takes a lot of computing power to run, making it unappealing for power-efficient neural video compression codecs. CABAC fares even worse, as symbols have to be decoded one at a time in order to get the right frequency table at each step.

There is another way! Asymmetric numeral systems (ANS) [6] combines the compression performance of arithmetic coding with the speed of Huffman coding. It operates on a similar principle to arithmetic coding, but instead of having to keep track of an interval of numbers, it directly operates on a single number. This development and the work that has followed it show that there are still practical improvements to be found in the field of lossless compression.

Further topics and recap

You may be wondering whether any of the above is different for video data rather than images. The answer is, essentially, no! The content might be different, as videos often just store what has changed between different frames rather than each frame in its entirety, but at its core it still consists of a sequence of some symbols that can have the abovementioned techniques applied to them in order to turn them into a compressed bitstream.

In fact, lossless compression algorithms are even used when we wish do to lossy compression; that is to say when we don't want to store or transmit an exact copy of the original data. Almost all image and video data that we come across on the internet is in fact lossily compressed. This is usually done with a paradigm called transform coding by applying the following steps:

1. Analysis: transform the input data to allow you to identify which aspects are most important in some sense
2. Quantisation: discard less important parts so that you are left with a sequence of symbols that contain the key information. The more you discard, the more you will be able to compress but the worse the quality will be
3. Lossless compression: apply your favourite lossless compression algorithm as described in this blog post! You now have a compressed bitstream for storage/transmission
4. Synthesis: when you want to view the image/video, apply a reverse transformation to (1). It will look slightly different to the original depending on how much was thrown away in the irreversible step (2)

The answer to the question of how best to transform the data and which parts we can throw away while still maintaining visual quality is what Deep Render's research team has spent its time perfecting (and we aren't quite ready to let everyone in on our secrets), but a performant implementation of a lossless compression algorithm is also important to actually generate a compressed bitstream in a real-world setting. We believe that this fascinating topic is under-studied in the neural compression literature and our work on it forms a part of our offerings of the world's first AI codec.

To conclude, the key takeaway from the range of lossless compression algorithms we have surveyed is that if the data we wish to compress has some structure, such as repeating patterns and/or some symbols being more common than others, we can exploit this to save space in storage and transmission. More sophisticated algorithms can get closer to the theoretical minimum than less sophisticated ones, but in traditional video codecs this often comes at the cost of high computing power requirements. Deep Render's hardware integration team have developed a highly optimised in-house implementation of a modern lossless compression technique for real-time encoding and decoding with optimal compression performance, thus having our cake and eating it too!

References

[1] T. Tsukiyama et al., "Method and system for data compression and restoration," United States Patent 4586027, Apr. 29 1986.
[2] J. Ziv, A. Lempel, "A universal algorithm for sequential data compression," in IEEE Transactions on Information Theory, vol. 23, no. 3, pp. 337-343, 1977.
[3] C. E. Shannon, "A Mathematical Theory of Communication," in The Bell System Technical Journal, vol. 27., no. 3, pp. 379-423, 1948
[4] D. Huffman, "A Method for the Construction of Minimum-Redundancy Codes," in Proceedings of the IRE, vol. 40, no. 9, pp. 1098-1101, 1952.
[5] R. Pasco, "Source coding algorithms for fast data compression," Ph.D. dissertation, Stanford University, 1976.
[6] J. Duda, "Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding," 2014.

Footnotes

* In JPEG, the thing which we apply the lossless encoding to is not the pixel values themselves, but instead a representation of the frequencies in each 8x8 block of pixels. This is done because the human eye has less sensitivity to high frequency details, so it is possible to get away with removing them (which corresponds to setting their representation to 0) without degrading the image quality too much. If many of the frequency components "in a row" are set to 0, run length encoding is very effective!

† The numbers are actually stored in binary, but the point stands

‡ Some, like AV1, use variations such as non-binary bases to avoid infringing on patents